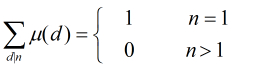莫比乌斯反演初步与实际应用

莫比乌斯反演初步和实际应用

定义和一般形式及其证明

假设有数论函数关系式$F(N) = \sum_{x|N}f(x)$，则有$f(N) = \sum_{x|N}\mu(x)F(\frac Nx) = \sum_{x|N}\mu(\frac xN)F(x)$

此为基本定义，但是看到这个函数也有限制就是必须是数论函数。，也就是定义域为正整数，对应集合为复数的函数。下面是函数的一般形式。

假设d定义在$[1,∞)$上的复值函数$G(N) = \sum_{x = 1}^NF(\frac Nx)$，则有$F(N) = \sum_{x = 1}^N\mu(x)G(\frac Nx)$

而这个$\mu(x)$函数就是莫比乌斯函数，其定义如下：

$x= 1$时，$\mu(x) = 1$。

$x = P_1P_2…P_M$，（$P$为互异素数），则$\mu(x) = (-1)^M$

其他情况下$\mu(x) = 0$

由定义可以得到莫比乌斯函数的两个重要性质：

对任意正整数$N$有$\sum_{x|N}\frac{\mu(x)}{x} = \frac{\varphi(N)}{N}$

证明 :

设有

$$\sum_{x|N}\mu(x) = [N = 1], f(N) = \sum_{x|N}[\frac Nx = 1]f(x)$$

代入得

$$f(N) = \sum_{x|N}\sum_{y|\frac Nx}\mu(y)f(x)$$

由于$\sum_{x|N}\sum_{y|\frac Nx}$的限制条件为$xy|N$，所以等式写成:

$$f(N) = \sum_{y|N}\mu(y)\sum_{x|\frac Ny}f(x) = \sum_{y|N}\mu(y)F(\frac Ny)$$

证明完毕。

代码实现

用线性筛法求莫比乌斯函数，时间复杂度$O(N)$

inline void Init() {
	memset(V, 0, sizeof(V)) ;
	Mu[1] = 1 ; Tot = 0 ;
}

inline void MU() {
	for (int i = 2 ; i < N ; i ++) {
		if (! V[i]) P[++ Tot] = i, Mu[i] = - 1 ;
		for (int j = 0 ; j <= Tot && P[j] < N ; j ++) {
			V[i * P[j]] = 1 ;
			if (i % P[j]) Mu[i * P[j]] = - Mu[i] ;
			else {Mu[i * P[j]] = 0 ; break ; }
		}
	}
}

例题：YY的GCD

给定$N, M$，求所有的$X \leq N,~Y \leq M$中$gcd(X, Y)$是质数的点对有多少对。

类似于一个模板题，因为其思维难度不是很大。考虑公式化题目描述，即求：$\sum_{X = 1}^N \sum_{Y = 1}^M [gcd(i,j) == P]$

设$f(x)​$为满足$gcd(X, Y) = X​$的$(X, Y)​$的对数，$F(X)​$为满足$X|gcd(X, Y)​$二点$(X, Y)​$的对数。得到

$$F(N) = \sum_{x|N}f(x)​$$

所以根据莫比乌斯反演定理，得​

$$f(N) = \sum_{x|N}\mu(\frac xN)F(x) =\sum_{x|N}\mu(\frac xN)\frac{N \times M}{X^2}​$$

而题目要求其$gcd(X,Y)$是一个质数也就是说

$$Ans = \sum_P^{min(N, M} \sum_i^N\sum_j^M[gcd(i,j) = P] = \sum_P^{Minn(N,M)}f(P)$$

设$T = PX$，则式子变为

$$\sum_{T = 1}^{Min(N,M)}\frac{N \times M}{T^2}(\sum_{G|T}\mu(\frac TG))$$

于是为了提高速度，可以预处理$\sum_{G|T}\mu(\frac TG)$。于是此题就以较快得速度解决了。

但是如果是多组数据还是有可能会$TLE$，所以如果想要更快，还可以使用整除分块。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std ;

typedef long long LL ;
const int MAXN = 10000010 ;

long long T, N, M, V[MAXN], P[MAXN], Mu[MAXN], Tot ;
long long S[MAXN], Ans, G[MAXN] ;

inline long long  Read() {
	long long X = 0, F = 1 ; char ch = getchar() ;
	while (ch > '9' || ch < '0') F = (ch == '-' ? - 1 : 1), ch = getchar() ;
	while (ch >= '0' && ch <= '9') X=(X<<1)+(X<<3)+(ch^48), ch = getchar() ;
	return X * F ;
}

inline void MU() {
	memset(V, 0, sizeof(V)) ;
	Mu[1] = 1 ; Tot = 0 ;
	for (int i = 2 ; i < MAXN ; i ++) {
		if (! V[i]) P[Tot ++] = i, Mu[i] = - 1, G[i] = 1 ;
		for (int j = 0 ; j < Tot && i * P[j] < MAXN ; j ++) {
			V[i * P[j]] = 1 ;
			if (i % P[j]) Mu[i * P[j]] = - Mu[i],
				G[i * P[j]] = Mu[i] - G[i] ; else {
				Mu[i * P[j]] = 0 ; G[i * P[j]] = Mu[i] ;
				break ;
			}
		}
	}
	for (int i = 1 ; i < MAXN ; i ++) S[i] = S[i - 1] + G[i] ;
}

int main() {
	MU() ;
	T = Read() ; while (T --) { 
		Ans = 0 ;
		N = Read(), M = Read() ; 
		for (int i = 1, j ; i <= min(N, M) ; i = j + 1) {
			j = min(N / (N / i), M / (M / i)) ;
			Ans += (N / i) * (M / i) * (S[j] - S[i - 1]) ;
		}
		printf("%lld\n", Ans) ;
	}
}